庭仕事と悟性 ― 2024年05月19日 16時15分30秒
アジサイの仲間である甘茶の花が咲き、山桜桃(ゆすらうめ)の実も少しずつ色づいてきました。この時期は植物がぐんぐん成長するので、ちょっと見ない間に庭の様子もずいぶん変わります。
それだけ庭仕事の忙しい時期で、殺伐とした最近のツイッター(X)でも、「庭仕事」で検索すると、日本中で庭仕事に励んでいる人たちの投稿がずらっと出てきて、しばし心がなごみます。私も狭い庭で汗を流すのが好きなので、大変だ大変だと口では言いながらも、それを十分楽しんでいます。
もちろん世の中には庭仕事が好きな人ばかりではありません。
親から相続した緑の濃い庭を、手入れが大変だという理由で、全面掘り起こしてコンクリートで固めた…という話も現に見聞きするので、そうした例を思えば、わが家の場合は庭にとっても、その主にとっても、幸せな関係だと言えると思います。
★
今から14年前、ヤフー知恵袋に某氏が投稿した質問【LINK】。
「長方形の面積についてですが、例えば長方形の周の長さを26cmとします。
縦11cm、横2cmとすると面積は、22平方cmとなります。
しかし同じ周の長さで、縦7cm、横6cmとすると面積は42平方cmとなります。
なぜ周の長さは、同じなのに比率を変えるだけで面積は変わるのでしょうか?
だれに聞いても答えられません。
だれか教えてください。」
縦11cm、横2cmとすると面積は、22平方cmとなります。
しかし同じ周の長さで、縦7cm、横6cmとすると面積は42平方cmとなります。
なぜ周の長さは、同じなのに比率を変えるだけで面積は変わるのでしょうか?
だれに聞いても答えられません。
だれか教えてください。」
そのベストアンサーはリンク先に書かれているので、興味のある方はご覧いただければと思います。
★
なんで唐突にこんな引用をしたかというと、わが家の庭仕事が(楽しいながらも)大変なのはなぜか?と考えたからです。
「庭仕事が大変だ」というと、「さぞお庭が広いのでしょうね」という反応をされる方もいると思うのですが、わが家の庭は言うまでもなく狭いです。しかし「長い」のです。
パースが簡単にとれるぐらい長くて、これはわが家が変形敷地、いわゆる旗竿地だからです。
狭いけれども長い…というのがこの場合味噌で、長ければ長いだけ、敷地境界沿いに植わっている植物も多くなり、それが多くの庭仕事を生んでいるわけです。ヤフー知恵袋が説く如く、周囲の長さが同じでも面積は異なる…つまり裏を返せば、同じ面積でも形状によって周囲の長さは大きく異なるのです。
(よく言えば「市中の山居」っぽい感じ)
★
余談に流れますが、この周囲の長さと面積に関連して、大変おもしろい論文を読みました。そもそも、人はなぜ上の知恵袋のような質問を発したくなるか?という点に関わるものです。
■西林克彦、「面積判断における周長の影響―その実態と原因―」
教育心理学研究 第36巻第2号(1988)、pp.120-128.
https://www.jstage.jst.go.jp/article/jjep1953/36/2/36_120/_pdf
教育心理学研究 第36巻第2号(1988)、pp.120-128.
https://www.jstage.jst.go.jp/article/jjep1953/36/2/36_120/_pdf
掲載誌名から分かる通り、教育心理学分野の論文です。その冒頭部より。
「ある図形の面積が、その周囲の長さ(周長)に影響されて誤判断されやすいことはよく知られている(銀林、1975)。とくに顕著 なのは周長が同じであると面積までが同一であるとみなされる傾向である。したがって小学校算数教科書に、その点に留意した記述が見られるものもある。細谷(1968)は、小学校2-4年生に周長を等しく保ちながら長方形を平行四辺形の形に押しつぶして面積の比較をさせ、各学年とも、面積は同じであって変わらないとする反応が過半数に達する結果を得たという。」
周長が等しければ面積も等しい…というのは、上の知恵袋で見たように、明らかに間違った考え方です。しかし小学生を被験者にして実験すると、そうした間違った考え方が2年生から4年生に至るまでずっと保持され続けている(つまりこの点では4年生も2年生と変わらない)という、不思議な結果を示しています。
著者・西林氏はこの点に焦点を当てて実験を重ね、その結論は以下のとおりです(太字は引用者)。
「周長の面積判断への影響は、面積概念の混乱や未成熟さに帰せられるものではないことは明らかである。それは保存の概念を経由して入り込んでくるのであり、成長し保存の概念を獲得したが故に誤るようになるのである。Bruner (Bruner et al., 1966) は、「成長によるエラー」を、「正確にいうなら、1つの表象システムと、いま1つの表象システムとの間に照応性や一致性をうちたてようとして、うまくゆかない最初の段階を示しているのである」として、表象システム間に限っているが、もっと一般化してよい概念だと思われる。」
つまり子供たちは成長につれて、見た目の変化に影響を受けない「保存」という概念を獲得し(これは高度に抽象的な概念です)、それを周長と面積の関係に不適切に応用してしまうため、結果的に誤った判断をしてしまうということです。ここで正しい判断を下すためには、さらにもう一段階成長を遂げる必要がありますが、次の段階にいけない人も多いことはヤフー知恵袋が証明しています。
★
上のことは人間理性のありようを考えるとき、きわめて示唆に富んだ話だと思いました。ひょっとして、人間がこの先いかに進化しようとも、神の視点からすれば同じようなことが繰り返されるのかもしれません。
庭仕事の合間にそんなことを考えました。
計算する骨 ― 2018年06月10日 07時15分27秒
スコットランドは、今はイギリスの一部ですが、「ランド」というぐらいですから、昔は独立した国で、イングランドと合併したのは1707年のことです。
その昔のスコットランド王国の貴族で、レオナルド的万能の科学者にして、オカルティズムの大家でもあった人に、ジョン・ネイピア(John Napier,、1550-1617)という人物がいます。(当時はこういう怪人的学者が多くて、イングランドにはジョン・ディー(1527-1609)という大物がいましたし、東に目を向ければ、奇想の皇帝・ルドルフ2世(1552-1612)のプラハ宮廷にも、何だかよく分からない人物が大勢出入りしていました。)
(ネイピアが住んだマーキストン城。右上はネイピアの部屋。19世紀の版画より。リンク先掲載の図を一部トリミング)
さて、そのネイピア。この才人の業績の中でも顕著なのは、数学分野におけるそれで、特に「対数」の発案者として、その名は不朽のものとなっています(とエラそうに書いていますが、この辺のことは他人の受け売りです)。あるいは、「対数」と聞くと身構える人(私もその一人)でも、彼が小数点の考案者だと聞けば、なるほど偉い人だと思うでしょう。
★
そして、彼の発明でもう1つ有名なのが、「ネイピアの骨(Napier's bones)」と呼ばれるものです。
(アメリカのArmstrong Metal Craft社製の現代の「ネイピアの骨」と解説書。表紙を飾るのはジョン・ネイピアの肖像)
洒落たオークの箱に、銀白色のステンレスに刻まれた数字が並んでいます。
中身は一枚板ではなくて、バラバラの四角い棒。
そして、箱の左側に彫られた1から9までの数字。
一体これは何か?
これはネイピアが発明した計算装置です。これさえあれば、桁数の多い掛け算を効率的に行うことができ、さらにそれを応用して、割り算や平方数、平方根まで計算できるという優れもの。(ちなみに、なぜ「骨」かといえば、昔は象牙を削った棒を使い、いかにも骨っぽい外観だったからです。)
なぜそんなことができるのか?
小学校時代に戻って、掛け算を筆算で行う場面を思い出してください。あそこで我々が行っていた作業は、結局「九九」と「足し算」だけです(よーく思い出してください)。ですから、たとえ九九を暗記していなくても、九九を教えてくれる補助装置さえあれば、足し算だけで、多桁の掛け算をこなせます。そして、ネイピアの骨とは、九九を教えてくれる補助装置に他なりません。
例えば、いちばん上を見ると、「4678539」と並んでいます。で、一番左の4の棒を下に見ていくと「4、8、12、16…」、その隣の6の棒は「6、12、18、24…」と数字が彫られています。言うまでもなく九九の答です。
この「4678539」というのは、実はウィキペディアの「ネイピアの骨」の項目に挙がっている計算例と同じ数字で、そこでは「4678539×7」を計算するやり方が、下の図とともに解説されています。
(左図の上から7段目(×7を意味します)に注目。それを拡大したのが右図)
実際に「4678539×7」を筆算で解く場面を想像しながら、この図を眺めると、ネイピアの骨の原理がお分かりいただけるでしょう。
さらに、「4678539×792」のような「多桁×多桁」の掛け算も同じことです。
1の位(上の例では2)、10の位(同じく9)、100の位(同じく7)…の順に、上のやり方で積を求め、それを一ケタずつずらして書き並べ、最後に足し算すれば答に到達できます(これまた筆算と同じ手順です)。
割り算のときは、「九九」と足し算に加えて、さらに引き算も必要になりますが、原理はそう変わりません。
(4678539÷96431の計算例)
ここでさらに平方数や平方根の計算も説明できるといいのですが、この辺になると、私の理解が胡乱(うろん)になってくるので、興味のある方は、上記のウィキペディアの解説を参照していただければと思います。
(平方数や平方根の計算には、通常の棒に加えて特別の棒を使います。左下に見える幅広の棒が、平方数計算用。似たような形をした平方根計算用の棒もあります。)
★
ネイピアのアイデアは、さらに歯車式のからくりと結びついて、世界初のメカニカル計算機を生み出しました。1623年に、ドイツのヴィルヘルム・シッカート(Wilhelm Schickard,1592-1635)が発明したのがそれです。
(6ケタ×1ケタの掛け算を自動でこなすシッカートの計算機(復元)。ウィキぺディア「ヴィルヘルム・シッカート」の項より)
シッカートは自らの計算機を、天文計算に使用することを想定し、それをケプラーに手紙で知らせていたそうですから、これは天文古玩的にも興味を覚える話です。
そして、ここから計算機の歴史は始まり、19世紀になると実用性を備えた多くの機械式計算機が製作され、社会の変化を加速しました。さらに、プログラムの考えが生まれ、機械式パーツが電子デバイスに置き換わり、今の社会があるわけです。
(ネイピアの骨の子孫たち。Armstrong Metal Craft社の解説書エピローグより)
★
ネイピアの骨は、数の世界の抽象美を具象美に変えて見せてくれているようです。
おさる計算機(下) ― 2018年06月08日 07時14分22秒
さて、教養ある猿のからくりを見てみましょう。
「おさる計算機」の裏側がどうなっているかというと…
何もありません。見事に何もありません。
あるのは、計算機を立てるスタンドだけです。
すなわち、メカニズムはすべて昨日見た表側にあったのです。
最初それに気づかず、「?」と思い、次に「!」と思いました。
この猿も賢いですが、これを作った人間もやっぱり賢いです。
ここには歯車やギアすらありません。このメカニズムを構成するのは、リベット留めした猿の関節に仕組まれたピボット機構のみです。
それによって、左右の足を閉じていけば…
スーッとポインターが下りていき…
ある特定の位置で止まります。
そして、この上下動に左右のスライド機構を組み合わせれば、
両足の位置を定めると、ポインターの位置は一義的に決まります。
あとは、そのポインターの位置に合わせて、答(2数の積)をあらかじめ印刷しておけば、みごとな計算機の出来上がりです。
知ってみれば「なーんだ」ですが、こういうのを「コロンブスの卵」と言うのでしょう。
★
このブリキの玩具は、元々1916年にアメリカで作られたもので(William Robertsonという人が特許を取りました)、手元にあるのは、それをドイツの玩具メーカーが復刻したものです。
おさる計算機(上) ― 2018年06月07日 07時15分11秒
おもちゃの話題は一服と書きましたが、再度おちゃめいた品を載せます。
(約14cm角のブリキ製)
でも、これを安易におもちゃ呼ばわりしてはいけません。
何せ、このめかしこんだ猿は、複雑な計算をたちどころにこなす、立派な計算機なのですから。そんなわけで、今日の記事のカテゴリーは「数学」です。
★
その操作法は、ごくシンプルです。
まず右足と左足で、掛け合わせたい二つの数を指定します。
たとえば、こんな具合に「4」と「9」に合わせると…
手先のインジケーターがするすると動いて、ぴたりと「36」を表示してくれます。
何と賢い猿なのでしょう。
そんなわけで、名称も「”Consul”, The Educated Monkey」。
まさに教養ある猿です。そして『コンサル』とくると、ちょっと猿が付きすぎですが、「コンサル」(今ではもっぱら「領事」の意です)には、「コンサルタント」と同義の古い用法があるので、ここでも「指南役」といった意味でしょう。
(背部のスタンドを使えば、頼もしい指南役を常に机上に置くことができます。)
★
問題は、これがどのような機構によって実現されているか、です。
電子デバイスに頼らず、歯車やギアといった機械部品だけで、この猿に計算能力を持たせるには…。どうです、分かりますか?
「おさる計算機」の裏側に潜むメカニズムの紹介は次回。
(この項つづく)
ネットの穴を覗く ― 2018年02月18日 12時31分55秒
インターネットには実に多くの情報が堆積しています。
でも、仮にその情報量が無限だとしても、「すべての」情報がそこに乗っかるわけではありません。ちょうど無限にあるはずの有理数だけでは、数直線は埋まらず、漏れ落ちる情報も、また無限であるようなものです。(これは先日コメントをいただいたzam20さんの「ミクロ・マクロ・時々風景」で拝読し、思わず膝を打った比喩。)
★
先日、飛行機乗りのための星座早見盤の話題を書きました。
それを受けて、今度は船乗りのための星図を探しました。探してみると、実際そういう航海用星図はたくさんあって、船乗りは海図片手に水平線を眺めるばかりでなく、星空にも親しんでいることが、改めてよく分かりました。
船乗りが眺めた星空の件は、また別に記事にしたいと思いますが、その手の星図を買ったら、売り手の人がオマケとして、マップ・ディバイダを付けてくれました。
マップ・ディバイダは、2本の脚を開閉して、地図上の任意の2点間の距離を拾い上げる器具です。コンパスタイプの品もありますが、これは上部の丸い部分を握ると脚が開くタイプ。これだと片手で操作できるので、すこぶる作業効率が良いです。
本命の星図は1947年刊行だったので、このディバイダも同年代のものかなと思いますが、最後まで分からなかったのは、その素性です。
ディバイダの最上部、両足の回転軸を留めるビスには、「W & HC」というメーカーの記載があります。また裏側には「BRITISH MADE」の刻印もありました。検索すると、この「W & HC」ブランドのディバイダは、新品・中古を含めて大量に売られており、時代も1930年代と称する品から、ごく最近の物にまで及びます。まあ、おまけに付けてくれるぐらいですから、品物の価値は最初から知れており、そう古いものでないことは確かですが、それでも、この「W & HC」とは何のイニシャルなのか、それだけでも知りたいと思いました。
で、早速調べたのですが、これだけ流通している「W & HC」の正体が杳として知れないのです。「まさか、そんなはずはない」と思って、いろいろ検索したのですが、まったく分かりませんでした(唯一このイニシャルで見つかったのは、Wallsend & Hebburn Coal Company という、50年前に廃業したスコットランドの石炭商だけした)。
★
ディバイダの正体はさておき、ことほど左様に、ネット情報には意外な穴がポコポコ開いています。裏返せば、ユニークな情報は意外と身近なところにゴロゴロしていて、今日も誰かに発見されるのをひそかに待っているのでしょう。
-----------------------------------------------------------
▼閑語(ブログ内ブログ)
昨日の記事を書いた後で、古武道の士にして、フリーランスの記者でもある瀬沼翠雨氏のブログ、「新・流れ武芸者のつぶやき」を拝読しました。その2月16日の記事、「メメント・モリ」に接し、深く歎息するとともに、大いに頷いたことがあります。
昨日の私は、ジャーナリズム退潮の背後に、権力者が使嗾(しそう)する後ろ暗い力の存在を憂慮しましたが、実はそこにはもっと即物的で、もっと暴力的な力が作用していたのです。
それはお金です。
今は活字商売がひどく左前だ…ということは承知していましたが、これほどの窮状にあるとは、瀬沼氏の文章を読むまで、実感していませんでした。かくて、その影響は業界の隅々にまで及び、今や老舗出版社であれ、大新聞社であれ、とにかく金になる仕事が先だ…というわけで、きわめて良識的な出版社であったはずの某社ですら、最近は“ネトウヨ本”に手を染めたりしているわけです。
もちろん、それが媒体の変化だけのことで、知性と人間主義に基づく言論空間が、新たにネット上に形作られているのならば、これほどの不安感は覚えないでしょうが、それもすこぶる怪しい気がしています。
【閑語のおまけ】
ときに昨日の「閑語」の末尾。唄を忘れたカナリアが棄てられるのは「後の山」でしたね。そして「裏の畑」で鳴くのはポチです。威勢よくジャーナリズム批判を展開したわりには、どうも知性と教養に欠ける記述でした。
ケプラーの入れ子(後編) ― 2016年12月16日 06時21分57秒
今回、ケプラーの太陽系モデルを注文したのは、現在ボストンを拠点に活躍している造形作家、バスシバ・グロスマンさんのサイトを通じてです。
■Bathsheba Sculpture http://bathsheba.com/
バスシバさんは、数学や科学の世界に登場する不思議な「かたち」の数々を、金属やレーザークリスタルで再現した作品を手がけていて、数年前にもガラスの銀河系モデルを紹介したことがあります。
化粧箱を開けると、8センチ角のガラスキューブが顔を出し、ケプラーのモデルはその内部に存在します。
なかなかこれが写真に撮りにくいのですが、真横から見ると下のような姿です。
正多面体の入れ子と、それを覆う球殻層――キューブの右下に見られるように、このモデルでは、全球ではなく半球としてそれが表現されています――が、ガラスの中に浮かんでいます。
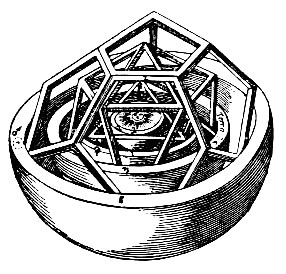
このモデルは、ちょうど上の図と同じ形になっていて、正十二面体とそれに外接する火星軌道までが表現されています。(さらに外側の木星と土星まで含めると、全体が大きくなり過ぎて、手で持てなくなるか、逆に中心部が小さくなり過ぎて、何だかわけが分からなくなるせいでしょう。)
微細な気泡が描く、ケプラーのイマジネーション。
裏返しにして、積み重なる球殻層を通して太陽系を眺めたところ。
なんと儚く、美しい宇宙モデルでしょうか。
なんと儚く、美しい宇宙モデルでしょうか。
400年前、天空を見上げるケプラーの目には、透明な球体と巨大な多面体がはっきりと見えていたはずです。
---------------------------------------------------------------
【閑語】(ブログ内ブログ)
最近の日本を見ていて思い浮かぶのは、「自己家畜化」という言葉です。
「自己家畜化」自体は、ヒトという生物種の特殊性を説明するための概念で、別にシニカルな意味は含まないのですが、どうも今の日本ではその域を超えて、急速に家畜化が進んでいるのではないか…と気懸りです。
「自己家畜化」自体は、ヒトという生物種の特殊性を説明するための概念で、別にシニカルな意味は含まないのですが、どうも今の日本ではその域を超えて、急速に家畜化が進んでいるのではないか…と気懸りです。
ケプラーの入れ子(前編) ― 2016年12月15日 10時50分31秒
お釈迦様がいみじくも説かれたように、人の生の本質は「苦」であり、この世はあらゆる業苦に満ちています。今の世界を見渡せば、その言葉の正しさをあえて否定できなかろうと思います。そして、人間の心のうちには、それとは反対のものを求める心がありますから、優しい光を投げかける満月を見上げれば、ふと欣求浄土の念がきざしたりします。昨夜は家路をたどりながら、そんな思いで月を眺めていました。
★
さて、ケプラーが「多面体の入れ子」として太陽系をイメージしたことは、これまで折に触れて記事のネタにしてきました。その中でわりとまとまっているのが以下の記事。
(画像再掲)
ケプラーの説をいちいち言葉にすれば、こういうことです。
☿ まず太陽の周囲を回る水星軌道を大円とする球を描いてごらん。
♀ 次にこの「水星球」に外接する正八面体と、それに外接する球を描いてごらん。
そこに金星軌道が浮かび上がるだろう。
そこに金星軌道が浮かび上がるだろう。
♁ 今度は「金星球」に外接する正二十面体と、それに外接する球を描いてごらん。
そこに地球軌道が浮かび上がるだろう。
そこに地球軌道が浮かび上がるだろう。
♂ 続けて「地球球」に外接する正十二面体と、それに外接する球を描いてごらん。
そこに火星軌道が浮かび上がるだろう。
そこに火星軌道が浮かび上がるだろう。
♃ さらに「火星球」に外接する正四面体と、それに外接する球を描いてごらん。
そこに木星軌道が浮かび上がるだろう。
そこに木星軌道が浮かび上がるだろう。
♄ 最後に「木星球」に外接する正六面体と、それに外接する球を描いてごらん。
そこに土星軌道が浮かび上がるだろう。
そこに土星軌道が浮かび上がるだろう。
…そして「土星球」の外側に、もはや惑星は存在しない。
なぜなら、正多面体はこの5種類でおしまいだからだ。これが宇宙の摂理なのだ。
なぜなら、正多面体はこの5種類でおしまいだからだ。これが宇宙の摂理なのだ。
★
もちろん土星外の惑星が発見された今、これは単なる奇説に過ぎません(もし発見されてなくたって、十分奇説でしょう)。
でも奇説にしても、ちょっと美しい奇説です。
この奇説を手に取って眺めたいと思い立ち、いろいろ探しました。
それが黒い箱に入って届いたので、ここで眺めておきます。
それが黒い箱に入って届いたので、ここで眺めておきます。

(後編につづく)
ソリッド感を求めて(後編) ― 2016年02月15日 06時25分20秒
ステレオスコープを応用した、立体幾何学の教材。
その解説冊子の裏表紙を見ると、
その解説冊子の裏表紙を見ると、
「完璧な新分野」、「全学級において、日々の授業を行うに際して立体写真を用いるべきことは明白。」、「まこと幾何学の教師にとって、一揃いの良き立体図を備えたステレオスコープ以上に有用な道具のあることを私は知らない。」
…というようなことを、幾何学の大家らしい人が特筆大書しています。
中身は25枚のカードから成り、各カードのサイズは、約9×18cm。
ニューヨークのステレオ写真メーカー、Underwood & Underwood 社が、1907年に発行したものです。
ニューヨークのステレオ写真メーカー、Underwood & Underwood 社が、1907年に発行したものです。
★
その内容はというと、前半は平面と直線の性質に関する『ユークリッド原論 第11巻』に含まれる、もろもろの命題(たとえば命題4、「交わる2直線に垂直な直線はそれらを通る平面にも垂直」など)を取り上げ、後半では、種々の立体図形の性質や、透視図の原理、球面座標の考え方などを取り上げています。
数学についてはいささか○○なので、その内容を詳しく語ることはしませんが、黒板に難しい図を骨折って描くよりも、ステレオビュアーでサクッと立体視できれば、先生も楽だし、生徒の理解も進むだろう…という期待の下に生まれた、20世紀の新教材です。
まあ、↑↑や↑程度の図ならば、あえて立体視するまでもなく、だいたいイメージできる気はしますが、それでも真っ白な空間に、抽象的な立体がふわっと浮かび上がる瞬間は、ちょっと感動的です。いわば抽象が具象化する感じです。
そして、こんな↑複雑な図でも、
ビュアーにセットして、
エイヤっと覗けば、
直線や曲線の相互関係は、文字通り一目瞭然。
★
ここに浮かび上がるソリッド感は、確かに真のソリッドとは程遠い幻影にすぎません。
でも、硬くて緻密な真にソリッドな物体にしたって、そう感じるのは、やっぱり人間の脳が生み出した幻にすぎない…という言い方もできます。
でも、硬くて緻密な真にソリッドな物体にしたって、そう感じるのは、やっぱり人間の脳が生み出した幻にすぎない…という言い方もできます。
ソリッド感を求めて(前編) ― 2016年02月14日 13時51分50秒
ペラペラの絵葉書が続いたので、この辺で何かソリッド感がほしいところ。
そこで、こんなものを載せます。
そこで、こんなものを載せます。
「なんだ、紙の本か。あんまりソリッドじゃないな…」
と思いつつ、手に取ると、
と思いつつ、手に取ると、
これは本ではなくて、紙のケースになっています。
「ふむふむ、この辺が一寸ソリッドかな…」
とさらに中身を取り出すと、
「ふむふむ、この辺が一寸ソリッドかな…」
とさらに中身を取り出すと、
中にはカードの束と冊子が入っています。
冊子のタイトルは、『ステレオスコープによる立体幾何学(solid geometry)』。
なるほど!これはソリッドですね。
ソリッド感(固体っぽさ)は薄いですが、自らソリッドを名乗るぐらいですから、これはもう立派にソリッド(立体的)です。しかも、それをステレオスコープで覗くとなれば、話はますます立体的になってきます。
(と話が十分ソリッドになったところで、この項つづく)
質素な定規セットと「時代」の気分 ― 2015年10月04日 13時40分11秒
おそらく1930~40年代にさかのぼるであろう、古い児童用の定規セット。
イギリスの売り手は、これをお父さんの遺品から見つけたそうです。
イギリスの売り手は、これをお父さんの遺品から見つけたそうです。
箱には少年の後姿と、「The “Pupil’s Own”」「Complete and Accurate」という文字。
前者がちょっと訳しにくいですが、「僕らの製図セット」「正確無比」といったところでしょう。訳はともかく、このクォーテーションマークに込められた気持ち―それを手にした子どものプライドと満足感―は、たいへんよく分かる気がします。
古びた金属の味わい。
この魚の定規(?)は、いったい何に使うんでしょうか。
★
8月から9月にかけてブログの更新を休んでいた時、「自分にとってのノスタルジーとは何だろう?」と考えていました。そして、そのときの気分にしっくり合ったのが、このセットでした。
それが何故か…というのは、曰く言い難いのですが、こういう質素な―あえて言えば貧し気な―風情に、私はひどく弱いところがあります。そこには一種の自己憐憫の情がまじっている気がするんですが、こういうのを前にすると、何だかいじらしいような、無性に涙ぐまれるような気分になります。
そこには、かつての自分の「貧」が、影を落としているのでしょう(まあ、今も貧しいんですが、子供の頃はもっと切実でした)。私が21世紀の規範から外れて、不要なモノを買い続けるのは、そこに慢性的な飢餓感があるせいだと思います。
とはいえ、貧しさの一方で、当時の自分が、とても充実していたのも確かです。
子供時代の自分が、そうとはっきり意識していたわけではありませんが、やはりあれも日本が右肩上がりだったからこその、一種の「時代の気分」だったのかもしれません。
子供時代の自分が、そうとはっきり意識していたわけではありませんが、やはりあれも日本が右肩上がりだったからこその、一種の「時代の気分」だったのかもしれません。
★
ところで、この定規が届いた時、余りに埃まみれだったので、ちょっと水洗いしたんですが、手を滑らせて取り落としたら、三角定規がストンと床に刺さり、そのまま直立。思わず総毛立ちました。
油断していると危険きわまりないですが、昔の子どもだったら、喜んで手裏剣遊びの道具にしたかも。























































最近のコメント