結晶海に漕ぎ出す(6)…ブラベー格子(中編) ― 2014年08月13日 23時42分53秒
(昨日のつづき。以下の記述には、意図せざるウソがまじってるかもしれません。とりあえず自分用に書きました。)
「格子説」では、鉱物の構造を説明するのに、積み上がったレンガではなしに、立体メッシュを思い浮かべます。メッシュの交点に描き込まれた小球が、鉱物を構成する「分子」であり、ワイヤーはその「配列規則(を視覚化したもの)」。
この2つが決まれば、鉱物の性質も自ずと決まる…という考え方です。

一つ注意しないといけないのは、ワイヤーはあくまでも分子の配列パターンを視覚的に表現したものに過ぎず、それ自体は何ら実体のない、仮構の線だということです。したがって、「分子」を結ぶように線を引いたのは、単に見やすさとか、作画の便のためであり、「分子」からずらして線を引いても、結晶の表現としては等価です(↓)。
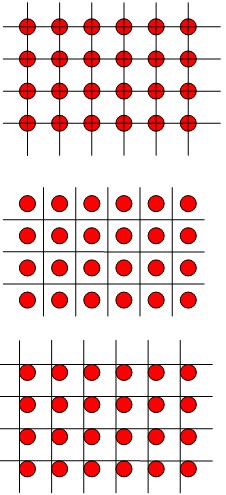
(ここでは簡略化して、結晶を2次元で表現しています。上・中・下段は、いずれも同一の結晶を表現するバリエーションに過ぎません。)
なお、ここで「分子」とカッコ書きしましたが、ここでいう「分子」は、科学的に正確な意味での分子ではありません。結晶学の分野では「基本構造」と言うそうですが、それは1個の原子(イオン)の場合もあり、また複数の分子が複雑に絡まっている場合もあり、要は結晶の中で繰り返されている基本パターンのことです。
下にそのイメージを模式的に示しました。
赤・黄・青・緑の4種の分子が、一定の間隔で並んでいますが、この場合、4つの分子を1セットにして「基本構造」と見なせます。上で述べたように、メッシュのワイヤーは、上のように表現しても、下のように表現しても構いません。
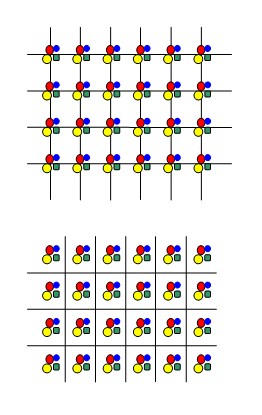
★
さて、ここで言葉の使い方を少し整理しておきます。
まず「格子(lattice)」とは、メッシュ構造の全体を指し、メッシュの1マス1マスは「単位格子(または単位胞 unit cell)」と呼ばれます。単位格子が縦横にズラッと並んで、結晶を形作っているわけです。
では、ここでメッシュの網目を、下の図のように粗くしてみたらどうでしょうか?
これも学問的には「あり」で、各マス目を並べると、ちゃんと結晶が出来上がるという意味で、やはり「単位格子」と呼ばれます。そして、上のように1つのマス目に1つの基本構造しか含まない場合は、特に「基本単位格子」と呼びます(何となく「基本」と「単位」の語感がかぶっていますが、 原語は「primitive unit cell」)。

(この場合も各マス目は「単位格子」)
★
ここで最初の図にもう一度登場してもらいます。

こういうメッシュ図を見ると、反射的に塩化ナトリウムの分子模型が思い浮かびます。
この両者をくらべて、もう一度「格子」の意味を確認してみます。
メッシュの交点(格子点)に存在する小球(基本構造)は、塩化ナトリウムの図でいうと何に当たるかお分かりでしょうか。
答はコレ↓ではなく、
コレ↓でもなく、
コレ↓です。
確かに、コレ↑でないと、上下・前後・左右にズラッと並べたときに、同じパターンの繰り返しにはなりません(この場合、各面は隣の基本構造と共用と考えてください)。
★
塩化ナトリウムは結晶系でいうと「立方晶」に属し、文字通り塩素とナトリウムが立方状に並んでいます。しかし、立方晶であることは、イコール原子(イオン)の配置が物理的に立方状であることを意味するわけではありません。
たとえば、ネット上を徘徊していて、「βマンガン」の結晶構造模型を見かけました。
(記憶の便のため、サムネイル画像をチラ貼りしておきます。詳細はリンク先をご覧ください。)

■Crystal lattice models:Explore Whipple Collection
http://www.hps.cam.ac.uk/whipple/explore/models/modellingchemistry/crystallatticemodels/
マンガンは、温度によって結晶構造が変わり、ここでモデル化しているのは、742~1095℃のときの「βマンガン」と呼ばれる状態です。そしてβマンガンには、さらに2つの原子配列があって、リンク先の模型では、赤と水色の球でそれを表現しています。
ここでは例えば赤い球のみに注目してもらえばよいですが、じっと凝視しても、そのどこにも立方パターンは浮かび上がりません。にも関わらず、βマンガンの基本構造に注目してメッシュをかぶせると、その形は黒いワイヤーによって表現される立方体となり、この立方体が無数に並び、積み重なることによってβマンガンは出来ています。そして、βマンガンも塩化ナトリウムと同じく、立派な立方晶の仲間なのです。
この例からも、「格子」の概念は、実際の分子配列よりも、抽象度が一段高いことが感じ取れると思います。
(大理石調のこの不定形な紋様も、よーく見ると正方形のメッシュをかぶせることができることにお気づきでしょう。結晶の中に潜む構造も、これと似たところがあります。)
★
結晶構造における「基本単位格子」の大雑把なイメージは以上のとおりです。
そして「ブラベー格子」とは、この基本単位格子を、その数学的性質に基づいて14種類に分類したものです。
では、その「数学的性質」とは何か?
(この項つづく)





最近のコメント